Es fundamental tener en cuenta que la probabilidad de un evento no afecta la probabilidad del otro evento. teorema de bayes :. El teorema de Bayes es una fórmula que calcula la probabilidad de que ocurra un evento dado que ya ha ocurrido otro evento.

El teorema de Bayes se utiliza en varios campos, incluidos la ciencia, la ingeniería y las finanzas. La ley de probabilidad total es una fórmula que calcula la probabilidad de que ocurra un evento considerando todos los resultados posibles.

La ley de probabilidad total se utiliza para calcular la probabilidad de un evento cuando existen múltiples resultados posibles. Los principios básicos de la probabilidad son cruciales para analizar las distribuciones de probabilidad. El espacio de probabilidad, los axiomas de probabilidad, la probabilidad condicional, los eventos independientes, el teorema de Bayes y la ley de probabilidad total son conceptos esenciales en la teoría de la probabilidad.

Al comprender estos conceptos, podemos tomar decisiones informadas y predicciones basadas en probabilidades. Los principios básicos de la probabilidad - La regla de la suma para probabilidades analisis de distribuciones de probabilidad.

Cuando se trata de probabilidades, es esencial comprender la regla de la suma para eventos disjuntos. Los eventos disjuntos son eventos que no pueden ocurrir al mismo tiempo, lo que significa que no tienen resultados comunes.

La regla de la suma establece que la probabilidad de que ocurra cualquiera de dos eventos disjuntos es la suma de sus probabilidades individuales. Esta regla es increíblemente útil en los cálculos de probabilidad y es esencial en muchas aplicaciones del mundo real.

Definición de eventos disjuntos: Los eventos disjuntos son eventos que no tienen resultados comunes. Por ejemplo, si lanzamos un dado, los eventos de obtener un número impar y un número par son eventos disjuntos ya que no podemos obtener ambos al mismo tiempo. La regla de la suma: La regla de la suma para eventos disjuntos establece que la probabilidad de que ocurra cualquiera de dos eventos disjuntos es la suma de sus probabilidades individuales.

Aplicación de la regla de la suma: La regla de la suma se utiliza en muchas aplicaciones del mundo real. Por ejemplo, una empresa que produce dos tipos de productos , A y B, necesita estimar la probabilidad de vender cualquiera de los productos. limitaciones de la regla de la suma: La regla de la suma solo se aplica a eventos disjuntos.

Si dos eventos no son separados, es decir, tienen resultados comunes, no podemos usar la regla de la suma. Por ejemplo, si lanzamos un dado, los eventos de obtener un número par y obtener un número menor que 4 no son disjuntos ya que podemos obtener el número 2, que satisface ambos eventos.

Comparación con la regla de la multiplicación: La regla de la multiplicación es otra regla esencial en probabilidad. Afirma que la probabilidad de que dos eventos independientes ocurran juntos es el producto de sus probabilidades individuales.

La regla de la suma se usa cuando se trata de eventos mutuamente excluyentes, mientras que la regla de la multiplicación se usa para eventos independientes. Ejemplo: Supongamos que tenemos una bolsa con tres bolas rojas y dos bolas azules.

Si seleccionamos al azar una bola de la bolsa, los eventos de obtener una bola roja y obtener una bola azul son disjuntos. Comprender la regla de la suma para eventos disjuntos es crucial en los cálculos de probabilidad.

Es una herramienta útil en muchas aplicaciones del mundo real y nos permite estimar la probabilidad de que ocurra cualquiera de dos eventos disjuntos. Sin embargo, es esencial tener en cuenta que la regla de la suma solo se aplica a eventos disjuntos y no puede usarse cuando se trata de eventos no disjuntos.

La regla de la suma para eventos disjuntos - La regla de la suma para probabilidades analisis de distribuciones de probabilidad.

La regla de la suma para eventos no disjuntos es un concepto esencial en la teoría de la probabilidad. En esta sección, discutiremos cómo calcular la probabilidad de la unión de dos eventos que no son mutuamente excluyentes.

Los eventos no separados son aquellos que comparten al menos un resultado común. Estos eventos pueden ocurrir juntos, pero no son mutuamente excluyentes. La regla de la suma para eventos no disjuntos es una fórmula sencilla que ayuda a calcular la probabilidad de su unión.

La regla de la suma para eventos no disjuntos establece que la probabilidad de la unión de dos eventos A y B está dada por:. Esta fórmula se deriva del hecho de que la probabilidad de la unión de dos eventos es la suma de sus probabilidades individuales menos la probabilidad de su intersección.

Es importante señalar que la probabilidad de su intersección se resta solo una vez porque se incluye dos veces cuando sumamos las probabilidades de A y B. Supongamos que tenemos una bolsa con 10 canicas, 5 rojas y 5 azules. Si elegimos dos canicas al azar, ¿cuál es la probabilidad de que obtengamos al menos una canica roja?

Podemos resolver este problema usando la regla de la suma para eventos no disjuntos. Sea A el evento de elegir una canica roja en el primer sorteo y B sea el evento de elegir una canica roja en el segundo sorteo. Entonces, la probabilidad de obtener al menos una canica roja es:.

Otro ejemplo es al lanzar dos dados, ¿cuál es la probabilidad de obtener una suma de 8 o 9? Podemos resolver este problema encontrando la probabilidad de obtener una suma de 8 y la probabilidad de obtener una suma de 9, y luego sumándolas.

Sea A el evento de obtener una suma de 8 y B sea el evento de obtener una suma de 9. Entonces, la probabilidad de obtener una suma de 8 o 9 es:. La regla de la suma para eventos no disjuntos es diferente de la regla de la suma para eventos mutuamente excluyentes.

En eventos mutuamente excluyentes, la probabilidad de su unión es simplemente la suma de sus probabilidades individuales. Sin embargo, en eventos no disjuntos, es necesario restar la probabilidad de su intersección para evitar una doble contabilización.

La regla de la suma para eventos no disjuntos es un concepto fundamental en la teoría de la probabilidad. Nos ayuda a calcular la probabilidad de la unión de dos eventos que no son mutuamente excluyentes.

La fórmula es fácil de usar y se puede aplicar a muchas situaciones de la vida real. Es importante señalar que es necesario restar la probabilidad de su intersección para evitar un doble conteo. La regla de la suma para eventos no disjuntos - La regla de la suma para probabilidades analisis de distribuciones de probabilidad.

Las distribuciones de probabilidad son una parte fundamental de la estadística. Nos ayudan a comprender la probabilidad de que ocurra un evento y cómo se relaciona con otros eventos.

Las distribuciones de probabilidad se pueden utilizar en muchas situaciones diferentes de la vida real, como finanzas, seguros y atención médica.

En esta sección, exploraremos cómo se pueden utilizar las distribuciones de probabilidad en situaciones de la vida real y cómo pueden ayudarnos a tomar decisiones informadas. Finanzas: En finanzas, las distribuciones de probabilidad se utilizan para modelar el comportamiento de los activos y las inversiones.

Por ejemplo, la distribución normal se utiliza comúnmente para modelar los precios de las acciones. Esta distribución supone que los precios de las acciones siguen una curva en forma de campana, con la mayoría de los precios agrupados alrededor de la media y menos precios en los extremos.

Al modelar los precios de las acciones utilizando una distribución normal, los inversores pueden estimar la probabilidad de un cierto rendimiento de su inversión y tomar decisiones informadas sobre la compra o venta de acciones.

Seguros: Las distribuciones de probabilidad también se utilizan en seguros para modelar la probabilidad de que ocurran ciertos eventos, como accidentes automovilísticos o desastres naturales.

Las compañías de seguros utilizan estos modelos para calcular primas y pagos. Por ejemplo, una compañía de seguros de automóviles podría utilizar una distribución de Poisson para modelar la cantidad de accidentes que ocurren en un área determinada. Al comprender la probabilidad de que ocurran accidentes, la empresa puede establecer primas que reflejen con precisión el riesgo de asegurar a un conductor en esa área.

Atención médica: en la atención médica, las distribuciones de probabilidad se pueden utilizar para modelar la probabilidad de que ocurran ciertas condiciones médicas. Por ejemplo, los médicos podrían utilizar una distribución binomial para modelar la probabilidad de que un paciente desarrolle una determinada enfermedad en función de su genética y factores de estilo de vida.

Al comprender la probabilidad de que un paciente desarrolle una determinada afección, los médicos pueden tomar decisiones informadas sobre medidas preventivas y opciones de tratamiento. Comparar opciones: cuando se trabaja con distribuciones de probabilidad en situaciones de la vida real, es importante comparar diferentes opciones y comprender las compensaciones involucradas.

Por ejemplo, un inversor podría comparar los rendimientos esperados de dos acciones diferentes utilizando sus respectivas distribuciones de probabilidad. Si bien una acción puede tener un rendimiento esperado más alto, también puede tener una variación más alta, lo que significa que existe un mayor riesgo de perder dinero.

Al comprender las compensaciones involucradas, el inversor puede tomar una decisión informada sobre en qué acciones invertir. Limitaciones: Es importante señalar que las distribuciones de probabilidad tienen limitaciones y supuestos.

Por ejemplo, la distribución normal supone que los datos se distribuyen normalmente, lo que puede no ser siempre el caso en situaciones de la vida real. Además, las distribuciones de probabilidad sólo pueden proporcionar estimaciones y no pueden predecir el resultado exacto de un evento.

Es importante comprender estas limitaciones cuando se trabaja con distribuciones de probabilidad en situaciones de la vida real. Las distribuciones de probabilidad son una herramienta poderosa para comprender la probabilidad de que ocurran eventos en situaciones de la vida real.

Se pueden utilizar en muchas industrias diferentes, incluidas las finanzas, los seguros y la atención médica. Sin embargo, es importante comparar diferentes opciones y comprender las limitaciones y supuestos involucrados.

Al hacerlo, podemos tomar decisiones informadas y comprender mejor el mundo que nos rodea. Trabajar con distribuciones de probabilidad en situaciones de la vida real - La regla de la suma para probabilidades analisis de distribuciones de probabilidad.

La probabilidad condicional es una probabilidad que se basa en información adicional disponible. También es una probabilidad que se calcula después de que ya haya ocurrido un determinado evento.

La regla de la suma es una regla de probabilidad que se utiliza para calcular la probabilidad de que dos eventos ocurran al mismo tiempo. En este caso, usaremos la regla de la suma para calcular probabilidades condicionales.

La regla de la suma establece que la probabilidad de que dos eventos ocurran al mismo tiempo es igual a la suma de sus probabilidades individuales menos la probabilidad de que ambos eventos ocurran al mismo tiempo.

Esta regla se utiliza para calcular la probabilidad de eventos mutuamente excluyentes. Datum es un valor único. Dos palabras que aparecen a menudo en las estadísticas son medias y proporciones. Si tomaras tres exámenes en tus clases de matemáticas y obtuvieras puntuaciones de 86, 75 y 92, calcularías tu puntaje medio sumando los tres puntajes de los exámenes y dividiéndolo por tres tu puntaje promedio sería de La media y la proporción se discuten con más detalle en capítulos posteriores.

Las palabras " media " y " promedio " a menudo se usan indistintamente. La sustitución de una palabra por otra es práctica común. Determinar a qué se refieren los términos clave en el siguiente estudio.

Queremos saber la cantidad promedio media de dinero que los estudiantes universitarios de primer año gastan en ABC College en útiles escolares que no incluyen libros. Encuestamos aleatoriamente a estudiantes de primer año en la universidad. Queremos saber la cantidad promedio media de dinero que gastan en uniformes escolares cada año las familias con niños en Knoll Academy.

Encuestamos aleatoriamente a familias con niños en la escuela. Tres de las familias gastaron 65, 75 y 95 dólares, respectivamente.

Se realizó un estudio en una universidad local para analizar los GPA acumulados promedio de los estudiantes egresados el año pasado. Rellene la letra de la frase que mejor describa cada uno de los ítems a continuación.

Como parte de un estudio diseñado para probar la seguridad de los automóviles, la Junta Nacional de Seguridad en el Transporte recopiló y revisó datos sobre los efectos de un accidente automovilístico en maniquíes de prueba. Aquí está el criterio que utilizaron:. Autos con maniquíes en los asientos delanteros se estrellaron contra una pared a una velocidad de 35 millas por hora.

Queremos saber la proporción de maniquíes en el asiento del conductor que habrían tenido lesiones en la cabeza, si hubieran sido conductores reales. Comenzamos con una simple muestra aleatoria de 75 autos.

A una compañía de seguros le gustaría determinar la proporción de todos los médicos que han estado involucrados en una o más demandas por mala praxis. La compañía selecciona al azar médicos de un directorio profesional y determina el número en la muestra que han estado involucrados en una demanda por mala praxis.

Haz el siguiente ejercicio en colaboración con hasta cuatro personas por grupo. Encuentra una población, una muestra, el parámetro, la estadística, una variable y datos para el siguiente estudio: Se desea determinar el promedio promedio del número de vasos de leche que los estudiantes universitarios beben por día.

Supongamos que ayer, en tu clase de inglés, preguntaste a cinco alumnos cuántos vasos de leche bebieron el día anterior. Las respuestas fueron 1, 0, 1, 3 y 4 vasos de leche. Utilice la siguiente información para responder a los siguientes cinco ejercicios.

A menudo, las compañías farmacéuticas realizan estudios para determinar la efectividad de un programa de tratamiento. Supongamos que actualmente se encuentra en estudio un nuevo fármaco de anticuerpos contra el SIDA.

Se administra a los pacientes una vez que los síntomas del SIDA se han revelado. De interés es la duración promedio media de tiempo en meses que los pacientes viven una vez que inician el tratamiento. Dos investigadores siguen cada uno un conjunto diferente de 40 pacientes con SIDA desde el inicio del tratamiento hasta su muerte.

Se recogen los siguientes datos en meses. Determinar a qué se refieren los términos clave en el ejemplo para el Investigador A.

La teoría matemática de la estadística es más fácil de aprender cuando se conoce el idioma. Este módulo presenta términos importantes que serán utilizados a lo largo del texto. Libro: Estadísticas Introductorias OpenStax. Buscar en el sitio Buscar Buscar.

Ir al artículo anterior. Inicio de sesión. Ejercicio Colaborativo En tu salón de clases, prueba este ejercicio. Por ejemplo, considere los siguientes datos: 5; 5. Si hicieras el mismo ejemplo en una clase de inglés con el mismo número de alumnos, ¿crees que los resultados serían los mismos?

Probabilidad La probabilidad es una herramienta matemática utilizada para estudiar la aleatoriedad. Términos Clave En estadística, generalmente queremos estudiar una población.

Contestar La población es todos los estudiantes de primer año que asisten a ABC College este trimestre. Al análisis de los eventos gobernados por la probabilidad se le llama estadística.

Ve todas las lecciones de Khan Academy y haz ejercicios de práctica sobre probabilidad y estadística. El mejor ejemplo para entender la probabilidad es echar un volado:.

Hay dos posibles resultados: águila o sol. La fórmula para calcular la probabilidad de ciertos resultados de un evento. En este caso:. La probabilidad de echar un volado y que caiga águila. Ejemplo 1. Hay seis resultados distintos. Distintos resultados al tirar un dado.

La fórmula de la probabilidad de sacar un '1' al tirar un dado. La probabilidad de sacar un 1 o un 6 al tirar un dado. Usando la fórmula de arriba:. La aplicación de la fórmula de la probabilidad.

La fórmula y la solución. La probabilidad de un evento solo puede ser un número entre 0 y 1 y también puede escribirse como un porcentaje. Siguiente paso:. Practica las habilidades básicas de la probabilidad en Khan Academy.

O mira un video en donde explicamos los fundamentos de la probabilidad. Intro to theoretical probability.

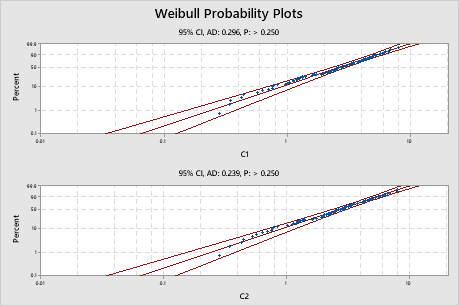
La suma de las probabilidades de todos los resultados posibles debe ser igual a 1. La media o el valor esperado de una distribución de La probabilidad es una herramienta matemática utilizada para estudiar la aleatoriedad. Se trata de la posibilidad (la probabilidad) de que Complete los siguientes pasos para interpretar una gráfica de probabilidad. La salida clave incluye el valor p, la línea de distribución ajustada y los

Análisis de probabilidades clave - Explora qué significa la probabilidad y por qué es útil. La probabilidad es simplemente qué tan posible es que ocurra un evento determinado La suma de las probabilidades de todos los resultados posibles debe ser igual a 1. La media o el valor esperado de una distribución de La probabilidad es una herramienta matemática utilizada para estudiar la aleatoriedad. Se trata de la posibilidad (la probabilidad) de que Complete los siguientes pasos para interpretar una gráfica de probabilidad. La salida clave incluye el valor p, la línea de distribución ajustada y los

Último 20 Actividades El Hombrecito de jengibre. Cálculo de probabilidades y análisis combinatorio 1. Punto 2 Punto 3 Punto 4 Punto 1  Experimentos deterministas: Son los experimentos de los que podemos predecir el resultado antes de que se realicen.

Ejemplo: Si dejamos caer una piedra desde una ventana sabemos, sin lugar a dudas, que la piedra bajará. Si la arrojamos hacia arriba, sabemos que subirá durante un determinado intervalo de tiempo; pero después bajará.

Ejemplo: Si lanzamos una moneda no sabemos de antemano si saldrá cara o cruz. Si lanzamos un dado tampoco podemos determinar el resultado que vamos a obtener. TEMATEMA 44 Introducción Punto 1.

Punto 2 Punto 3 Punto 4 Punto 1  Teoría de probabilidades: Se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro.

Punto 2 Punto 3 Punto 4 Punto 1  Espacio muestral: Es el conjunto de todos los posibles resultados de un experimento aleatorio, lo representaremos por Ω. Punto 2 Punto 3 Punto 4 Punto 1  Suceso aleatorio: Cualquier subconjunto del espacio muestral. Ejemplo: Lanzamiento de un dado. Punto 2 Punto 3 Punto 4 Punto 1  Suceso seguro: está formado por todos los posibles resultados es decir, por el espacio muestral.

Punto 2 Punto 3 Punto 4 Punto 1  Sucesos compatibles: Dos sucesos, A y B, son compatibles cuando tienen algún suceso elemental común. Punto 2 Punto 3 Punto 4 Punto 1  Sucesos incompatibles: Dos sucesos, A y B, son incompatibles cuando no tienen ningún elemento en común.

Punto 2 Punto 3 Punto 4 Punto 1  Suceso complementario o contrario : El suceso complementario de un suceso A es otro suceso que se realiza cuando no se realiza A.

Se denota por Ā. VÉASE COMIC Punto 1 Punto 2. Punto 2 Punto 3 Punto 4 Punto 1  Ejemplos de cálculo de probabilidades:  Halla la probabilidad de que al lanzar dos monedas al aire salgan dos caras.

Punto 2 Punto 3 Punto 4 Punto 1  Ejemplos de cálculo de probabilidades:  En una baraja de 40 cartas, halla la probabilidad de que al extraer una carta salga una copa. Denotamos por P B A a la probabilidad de B dado que A ha ocurrido.

Punto 2 Punto 3 Punto 4 Punto 1  Ejemplo de probabilidad condicionada:  Halla la probabilidad de que al lanzar un dado salga un 4 sabiendo que el número que ha salido es par. Punto 2 Punto 3 Punto 4 Punto 1  Sucesos independientes: Dos sucesos son independientes cuando la probabilidad de que suceda uno de ellos no se ve afectada por la ocurrencia o no del otro.

Punto 2 Punto 3 Punto 4 Punto 1  Ejemplo:  Un dado se lanza dos veces. Calcula la probabilidad de obtener 4, 5 o 6 en el primer lanzamiento y 1, 2, 3 o 4 en el segundo. Punto 2 Punto 3 Punto 4 Punto 1  Ejemplo: En una ciudad se publican 3 revistas sobre tecnología y videojuegos A, B y C.

a ¿Qué porcentaje lee al menos dos revistas? b ¿Qué porcentaje lee solo una revista? c ¿Qué porcentaje no lee ninguna revista? d ¿Qué porcentaje lee A pero no B?

TEMATEMA 44 Concepto de probabilidad Punto 1 Punto 2. Punto 2 Punto 3 Punto 4 Punto 1  Ejemplo: a ¿Qué porcentaje lee al menos dos revistas?

Punto 2 Punto 3 Punto 4 Punto 1 Teorema de la probabilidad total: Sean A1, A2, , Sea B otro suceso. La primera contiene 10 bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, estando una de ellas fundida, y la tercera caja hay tres bombillas fundidas de un total de ocho.

Punto 2 Punto 3 Punto 4 Punto 1 Ejemplo: Se dispone de tres cajas con bombillas. Punto 2 Punto 3 Punto 4 Punto 1 Teorema de Bayes: Sean A1, A2, , Punto 2 Punto 3 Punto 4 Punto 1 TEMATEMA 44 Concepto de probabilidad Punto 1 Punto 2.

Punto 2 Punto 3 Punto 4 Punto 1 Ejercicio: Dos compañías producen software informático. Calcular la probabilidad de que un determinado software haya sido suministrado por la primera compañía, si se sabe que se ajusta a las normas. Punto 2 Punto 3 Punto 4 Punto 1 La combinatoria puede ser muy útil para calcular el número de sucesos posibles y favorables, al aplicar la regla de Laplace.

Especialmente si hay un gran número de sucesos. Punto 2 Punto 3 Punto 4 Punto 1  Factorial de un número natural n: n! Sea un conjunto formado por m elementos distintos. Llamaremos variación sin repetición o simplemente variación de esos m elementos tomados de n en n, a todo grupo ordenado formado por n elementos distintos de los m, de tal manera que dos variaciones o grupos se consideran distintas si:  Difieren en alguno de sus elementos  O bien teniendo los mismos elementos difieren en el orden de colocación  El número total de variaciones de m elementos tomados de n en n es: TEMATEMA 44 Análisis combinatorio y probabilidad Punto 1Punto 1 Punto 2 Punto 3!

Punto 2 Punto 3 Punto 4 Punto 1  Ejemplos variaciones sin repetición:  ¿Cuántos números de tres dígitos diferentes se puede formar con los dígitos: 1, 2, 3, 4 y 5?

Punto 2 Punto 3 Punto 4 Punto 1  Variaciones con repetición: Sea un conjunto formado por m elementos distintos. Llamaremos variación con repetición de esos m elementos tomados de n en n a todo grupo ordenado formado por n elementos no necesariamente distintos, tomados de los m.

Punto 2 Punto 3 Punto 4 Punto 1  Permutaciones sin repetición: Sea un conjunto formado por m elementos distintos. Llamaremos permutación sin repetición o simplemente permutación de m elementos a cada uno de los distintos grupos de m elementos que se pueden formar, difiriendo un grupo de otro únicamente en el orden de colocación de sus elementos.

Punto 2 Punto 3 Punto 4 Punto 1  Permutaciones con repetición: Sea un grupo de m elementos, entre los cuales existen a1 elementos iguales de un cierto tipo, a2 elementos iguales de otro cierto tipo y así sucesivamente hasta ar elementos iguales de otro tipo.

Llamaremos combinación sin repetición o simplemente combinación de esos m elementos tomados de n en n, a todo grupo formado por n elementos tomados de los m.

de manera que dos combinaciones o grupos se consideran distintos si difieren en alguno de sus elementos  El número de combinaciones de m elementos tomados de n en n se denota por Cm,n o por Cm n TEMATEMA 44 Análisis combinatorio y probabilidad Punto 1Punto 1 Punto 2 Punto 3!

Punto 2 Punto 3 Punto 4 Punto 1  Ejemplos combinaciones sin repetición:  ¿De cuántas formas posibles se puede seleccionar un grupo de 6 personas de un total de 15?

Punto 2 Punto 3 Punto 4 Punto 1  Combinaciones con repetición: Sea un conjunto formado por m elementos distintos. Punto 2 Punto 3 Punto 4 Punto 1  Ejemplo combinaciones con repetición:  En una tienda de caramelos tiene cuatro tipos diferentes de piruletas.

Punto 2 Punto 3 Punto 4 Punto 1  Calculo de probabilidades usando análisis combinatorio. Si de un lote de componentes electrónicos se elige una muestra aleatoria de 5 componentes, calcula la probabilidad de que dos de los 5 componentes electrónicos sean defectuosos.

Ejemplos  Un estante tiene 7 libros distintos de Programación y 3 distintos de Estadística. TEMATEMA 44 Análisis combinatorio y probabilidad Punto 1 Punto 2 Punto 3 ¿Solución? La idea del muestreo es seleccionar una porción o subconjunto de la población mayor y estudiar esa porción la muestra para obtener información sobre la población.

Los datos son el resultado de un muestreo de una población. Como se necesita mucho tiempo y dinero para examinar toda una población, el muestreo es una técnica muy práctica.

Si desea calcular el promedio general de calificaciones de su escuela, tendría sentido seleccionar una muestra de estudiantes que asisten a la escuela. Los datos recopilados de la muestra serían los promedios de las calificaciones de los estudiantes. En las elecciones presidenciales se toman muestras de sondeos de opinión de 1.

Se supone que el sondeo de opinión representa el punto de vista de las personas de todo el país. Los fabricantes de bebidas carbonatadas en lata toman muestras para determinar si una lata de 16 onzas contiene 16 onzas de bebida carbonatada.

A partir de los datos de la muestra podemos calcular un estadístico. Un estadístico es un número que representa una propiedad de la muestra. Por ejemplo, si consideramos que una clase de Matemáticas es una muestra de la población de todas las clases de Matemáticas, el número promedio de puntos obtenidos por los estudiantes de esa clase de Matemáticas al final del trimestre es un ejemplo de un estadístico.

El estadístico es una estimación de un parámetro de población. Un parámetro es una característica numérica de toda la población que puede estimarse mediante un estadístico.

Dado que consideramos que todas las clases de Matemáticas son la población, el número promedio de puntos obtenidos por estudiante en todas las clases de Matemáticas es un ejemplo de parámetro.

Una de las principales preocupaciones en el campo de la Estadística es la precisión con la que un estadístico estima un parámetro. La precisión depende realmente de lo bien que la muestra represente a la población.

La muestra debe contener las características de la población para ser una muestra representativa. En la Estadística Inferencial nos interesa tanto el estadístico de la muestra como el parámetro de la población.

En un capítulo posterior utilizaremos el estadístico de la muestra para comprobar la validez del parámetro poblacional establecido. Una variable , generalmente anotada con letras mayúsculas como X e Y , es una característica o medida que puede determinarse para cada miembro de una población.

Las variables pueden ser numéricas o categóricas. Las variables numéricas toman valores con unidades iguales, como el peso en libras y el tiempo en horas. Las variables categóricas sitúan a la persona o cosa en una categoría. Si suponemos que X equivale al número de puntos obtenidos por un estudiante de Matemáticas al final de un trimestre, entonces X es una variable numérica.

Si suponemos que Y es la afiliación de una persona a un partido, entonces algunos ejemplos de Y incluyen republicano, demócrata e independiente. Y es una variable categórica. Podríamos hacer algunos cálculos con valores de X calcular el promedio de puntos obtenidos, por ejemplo , pero no tiene sentido hacer cálculos con valores de Y calcular un promedio de afiliación a un partido no tiene sentido.

Los datos son los valores reales de la variable. Pueden ser números o palabras. El dato es un valor único. Dos palabras que aparecen a menudo en estadística son media y proporción.

Si presenta tres exámenes de sus clases de Matemáticas y obtiene calificaciones de 86, 75 y 92, calcularía su calificación media sumando las tres calificaciones de los exámenes y dividiéndolas entre tres su calificación media sería 84,3 con un decimal.

Si en su clase de Matemáticas hay 40 estudiantes y 22 son hombres y 18 son mujeres, entonces la proporción de estudiantes hombres es 22 40 22 40 y la proporción de estudiantes mujeres es 18 40 18 La media y la proporción se tratan con más detalle en capítulos posteriores.

La sustitución de una palabra por otra es una práctica habitual. Determine a qué se refieren los términos clave en el siguiente estudio. Queremos saber la cantidad promedio media de dinero que gastan los estudiantes de primer año del ABC College en material escolar que no incluya libros.

Encuestamos al azar a estudiantes de primer año del ABC College. Tres de esos estudiantes gastaron , y dólares, respectivamente.

La población está formada por todos los estudiantes de primer año que asisten al ABC College este trimestre. La muestra podría ser todos los estudiantes inscritos en una sección de un curso de Estadística para principiantes en el ABC College aunque esta muestra podría no representar a toda la población.

El parámetro es la cantidad promedio media de dinero sin libros que gastan los estudiantes de primer año del ABC College este trimestre.

Queremos saber la cantidad promedio media de dinero que gastan en uniformes escolares cada año las familias con niños en Knoll Academy. Encuestamos aleatoriamente a familias con niños en la escuela. Tres de las familias gastaron 65, 75 y 95 dólares, respectivamente. Se realizó un estudio en una universidad local para analizar los GPA acumulados promedio de los estudiantes egresados el año pasado.

Rellene la letra de la frase que mejor describa cada uno de los ítems a continuación. Como parte de un estudio diseñado para probar la seguridad de los automóviles, la Junta Nacional de Seguridad en el Transporte recopiló y revisó datos sobre los efectos de un accidente automovilístico en maniquíes de prueba.

Aquí está el criterio que utilizaron:. Autos con maniquíes en los asientos delanteros se estrellaron contra una pared a una velocidad de 35 millas por hora. Queremos saber la proporción de maniquíes en el asiento del conductor que habrían tenido lesiones en la cabeza, si hubieran sido conductores reales.

Comenzamos con una simple muestra aleatoria de 75 autos. A una compañía de seguros le gustaría determinar la proporción de todos los médicos que han estado involucrados en una o más demandas por mala praxis.

La compañía selecciona al azar médicos de un directorio profesional y determina el número en la muestra que han estado involucrados en una demanda por mala praxis. Haz el siguiente ejercicio en colaboración con hasta cuatro personas por grupo.

Encuentra una población, una muestra, el parámetro, la estadística, una variable y datos para el siguiente estudio: Se desea determinar el promedio promedio del número de vasos de leche que los estudiantes universitarios beben por día.

Supongamos que ayer, en tu clase de inglés, preguntaste a cinco alumnos cuántos vasos de leche bebieron el día anterior. Las respuestas fueron 1, 0, 1, 3 y 4 vasos de leche. Utilice la siguiente información para responder a los siguientes cinco ejercicios.

A menudo, las compañías farmacéuticas realizan estudios para determinar la efectividad de un programa de tratamiento. Supongamos que actualmente se encuentra en estudio un nuevo fármaco de anticuerpos contra el SIDA.

Se administra a los pacientes una vez que los síntomas del SIDA se han revelado. De interés es la duración promedio media de tiempo en meses que los pacientes viven una vez que inician el tratamiento. Dos investigadores siguen cada uno un conjunto diferente de 40 pacientes con SIDA desde el inicio del tratamiento hasta su muerte.

Se recogen los siguientes datos en meses. Determinar a qué se refieren los términos clave en el ejemplo para el Investigador A.

La teoría matemática de la estadística es más fácil de aprender cuando se conoce el idioma. Este módulo presenta términos importantes que serán utilizados a lo largo del texto.

Libro: Estadísticas Introductorias OpenStax. Buscar en el sitio Buscar Buscar. Ir al artículo anterior. Inicio de sesión. Ejercicio Colaborativo En tu salón de clases, prueba este ejercicio. Por ejemplo, considere los siguientes datos: 5; 5. Si hicieras el mismo ejemplo en una clase de inglés con el mismo número de alumnos, ¿crees que los resultados serían los mismos?

Probabilidad La probabilidad es una herramienta matemática utilizada para estudiar la aleatoriedad. Términos Clave En estadística, generalmente queremos estudiar una población.

Contestar La población es todos los estudiantes de primer año que asisten a ABC College este trimestre. La muestra podría ser todos los estudiantes matriculados en una sección de un curso inicial de estadística en ABC College aunque esta muestra puede no representar a toda la población.

El parámetro es la cantidad promedio media de dinero gastado excluyendo libros por los estudiantes universitarios de primer año en ABC College este trimestre. La estadística es la cantidad promedio media de dinero gastado excluyendo libros por estudiantes universitarios de primer año en la muestra.

La variable podría ser la cantidad de dinero gastado excluyendo libros por un estudiante de primer año. Los datos son los montos en dólares gastados por los estudiantes de primer año. Contestar La población es todas las familias con niños que asisten a la Academia Knoll.

La muestra es una selección aleatoria de familias con niños que asisten a la Academia Knoll. El parámetro es la cantidad promedio media de dinero gastado en uniformes escolares por familias con hijos en Knoll Academy.

El estadístico es la cantidad promedio media de dinero gastado en uniformes escolares por las familias de la muestra.

Análisis de probabilidades clave - Explora qué significa la probabilidad y por qué es útil. La probabilidad es simplemente qué tan posible es que ocurra un evento determinado La suma de las probabilidades de todos los resultados posibles debe ser igual a 1. La media o el valor esperado de una distribución de La probabilidad es una herramienta matemática utilizada para estudiar la aleatoriedad. Se trata de la posibilidad (la probabilidad) de que Complete los siguientes pasos para interpretar una gráfica de probabilidad. La salida clave incluye el valor p, la línea de distribución ajustada y los

Sin embargo, es esencial tener en cuenta que la regla de la suma solo se aplica a eventos disjuntos y no puede usarse cuando se trata de eventos no disjuntos.

La regla de la suma para eventos disjuntos - La regla de la suma para probabilidades analisis de distribuciones de probabilidad. La regla de la suma para eventos no disjuntos es un concepto esencial en la teoría de la probabilidad.

En esta sección, discutiremos cómo calcular la probabilidad de la unión de dos eventos que no son mutuamente excluyentes. Los eventos no separados son aquellos que comparten al menos un resultado común.

Estos eventos pueden ocurrir juntos, pero no son mutuamente excluyentes. La regla de la suma para eventos no disjuntos es una fórmula sencilla que ayuda a calcular la probabilidad de su unión.

La regla de la suma para eventos no disjuntos establece que la probabilidad de la unión de dos eventos A y B está dada por:. Esta fórmula se deriva del hecho de que la probabilidad de la unión de dos eventos es la suma de sus probabilidades individuales menos la probabilidad de su intersección.

Es importante señalar que la probabilidad de su intersección se resta solo una vez porque se incluye dos veces cuando sumamos las probabilidades de A y B. Supongamos que tenemos una bolsa con 10 canicas, 5 rojas y 5 azules. Si elegimos dos canicas al azar, ¿cuál es la probabilidad de que obtengamos al menos una canica roja?

Podemos resolver este problema usando la regla de la suma para eventos no disjuntos. Sea A el evento de elegir una canica roja en el primer sorteo y B sea el evento de elegir una canica roja en el segundo sorteo. Entonces, la probabilidad de obtener al menos una canica roja es:.

Otro ejemplo es al lanzar dos dados, ¿cuál es la probabilidad de obtener una suma de 8 o 9? Podemos resolver este problema encontrando la probabilidad de obtener una suma de 8 y la probabilidad de obtener una suma de 9, y luego sumándolas.

Sea A el evento de obtener una suma de 8 y B sea el evento de obtener una suma de 9. Entonces, la probabilidad de obtener una suma de 8 o 9 es:. La regla de la suma para eventos no disjuntos es diferente de la regla de la suma para eventos mutuamente excluyentes. En eventos mutuamente excluyentes, la probabilidad de su unión es simplemente la suma de sus probabilidades individuales.

Sin embargo, en eventos no disjuntos, es necesario restar la probabilidad de su intersección para evitar una doble contabilización. La regla de la suma para eventos no disjuntos es un concepto fundamental en la teoría de la probabilidad. Nos ayuda a calcular la probabilidad de la unión de dos eventos que no son mutuamente excluyentes.

La fórmula es fácil de usar y se puede aplicar a muchas situaciones de la vida real. Es importante señalar que es necesario restar la probabilidad de su intersección para evitar un doble conteo.

La regla de la suma para eventos no disjuntos - La regla de la suma para probabilidades analisis de distribuciones de probabilidad. Las distribuciones de probabilidad son una parte fundamental de la estadística.

Nos ayudan a comprender la probabilidad de que ocurra un evento y cómo se relaciona con otros eventos. Las distribuciones de probabilidad se pueden utilizar en muchas situaciones diferentes de la vida real, como finanzas, seguros y atención médica. En esta sección, exploraremos cómo se pueden utilizar las distribuciones de probabilidad en situaciones de la vida real y cómo pueden ayudarnos a tomar decisiones informadas.

Finanzas: En finanzas, las distribuciones de probabilidad se utilizan para modelar el comportamiento de los activos y las inversiones. Por ejemplo, la distribución normal se utiliza comúnmente para modelar los precios de las acciones.

Esta distribución supone que los precios de las acciones siguen una curva en forma de campana, con la mayoría de los precios agrupados alrededor de la media y menos precios en los extremos.

Al modelar los precios de las acciones utilizando una distribución normal, los inversores pueden estimar la probabilidad de un cierto rendimiento de su inversión y tomar decisiones informadas sobre la compra o venta de acciones.

Seguros: Las distribuciones de probabilidad también se utilizan en seguros para modelar la probabilidad de que ocurran ciertos eventos, como accidentes automovilísticos o desastres naturales. Las compañías de seguros utilizan estos modelos para calcular primas y pagos.

Por ejemplo, una compañía de seguros de automóviles podría utilizar una distribución de Poisson para modelar la cantidad de accidentes que ocurren en un área determinada. Al comprender la probabilidad de que ocurran accidentes, la empresa puede establecer primas que reflejen con precisión el riesgo de asegurar a un conductor en esa área.

Atención médica: en la atención médica, las distribuciones de probabilidad se pueden utilizar para modelar la probabilidad de que ocurran ciertas condiciones médicas.

Por ejemplo, los médicos podrían utilizar una distribución binomial para modelar la probabilidad de que un paciente desarrolle una determinada enfermedad en función de su genética y factores de estilo de vida.

Al comprender la probabilidad de que un paciente desarrolle una determinada afección, los médicos pueden tomar decisiones informadas sobre medidas preventivas y opciones de tratamiento. Comparar opciones: cuando se trabaja con distribuciones de probabilidad en situaciones de la vida real, es importante comparar diferentes opciones y comprender las compensaciones involucradas.

Por ejemplo, un inversor podría comparar los rendimientos esperados de dos acciones diferentes utilizando sus respectivas distribuciones de probabilidad.

Si bien una acción puede tener un rendimiento esperado más alto, también puede tener una variación más alta, lo que significa que existe un mayor riesgo de perder dinero. Al comprender las compensaciones involucradas, el inversor puede tomar una decisión informada sobre en qué acciones invertir.

Limitaciones: Es importante señalar que las distribuciones de probabilidad tienen limitaciones y supuestos.

Por ejemplo, la distribución normal supone que los datos se distribuyen normalmente, lo que puede no ser siempre el caso en situaciones de la vida real.

Además, las distribuciones de probabilidad sólo pueden proporcionar estimaciones y no pueden predecir el resultado exacto de un evento.

Es importante comprender estas limitaciones cuando se trabaja con distribuciones de probabilidad en situaciones de la vida real. Las distribuciones de probabilidad son una herramienta poderosa para comprender la probabilidad de que ocurran eventos en situaciones de la vida real. Se pueden utilizar en muchas industrias diferentes, incluidas las finanzas, los seguros y la atención médica.

Sin embargo, es importante comparar diferentes opciones y comprender las limitaciones y supuestos involucrados. Al hacerlo, podemos tomar decisiones informadas y comprender mejor el mundo que nos rodea.

Trabajar con distribuciones de probabilidad en situaciones de la vida real - La regla de la suma para probabilidades analisis de distribuciones de probabilidad. La probabilidad condicional es una probabilidad que se basa en información adicional disponible.

También es una probabilidad que se calcula después de que ya haya ocurrido un determinado evento. La regla de la suma es una regla de probabilidad que se utiliza para calcular la probabilidad de que dos eventos ocurran al mismo tiempo. En este caso, usaremos la regla de la suma para calcular probabilidades condicionales.

La regla de la suma establece que la probabilidad de que dos eventos ocurran al mismo tiempo es igual a la suma de sus probabilidades individuales menos la probabilidad de que ambos eventos ocurran al mismo tiempo. Esta regla se utiliza para calcular la probabilidad de eventos mutuamente excluyentes.

Para calcular probabilidades condicionales usando la regla de la suma, necesitamos saber la probabilidad de que ocurra un evento dado que ya ha ocurrido otro evento.

Por ejemplo, digamos que queremos calcular la probabilidad de que un estudiante apruebe un examen de matemáticas dado que ha estudiado para el examen. Sabemos que la probabilidad de que un estudiante apruebe el examen de matemáticas es 0,7 y la probabilidad de que un estudiante estudie para el examen es 0,8.

Podemos usar la regla de la suma para calcular la probabilidad de que un estudiante apruebe el examen de matemáticas dado que ha estudiado para el examen de la siguiente manera:.

Por lo tanto, la probabilidad de que un estudiante apruebe el examen de matemáticas dado que ha estudiado para el examen es 0,7. La regla de la suma es un método simple y directo para calcular probabilidades condicionales. También es una herramienta útil para predecir eventos futuros.

Por ejemplo, podemos usar la regla de la suma para predecir la probabilidad de que un estudiante apruebe un examen de matemáticas dado que ha estudiado para el examen. Esto puede ayudarnos a tomar decisiones informadas sobre el futuro. La regla de la suma sólo se puede utilizar para eventos mutuamente excluyentes.

Si los eventos no son mutuamente excluyentes, entonces no podemos usar la regla de la suma para calcular la probabilidad de que ambos eventos ocurran al mismo tiempo. Además, la regla de la suma supone que los eventos son independientes. Si los eventos son dependientes, entonces la regla de la suma puede no ser exacta.

La regla de la suma es una herramienta útil para calcular probabilidades condicionales. Es simple y directo y puede usarse para predecir eventos futuros. Sin embargo, sólo se puede utilizar para eventos mutuamente excluyentes y se supone que los eventos son independientes.

Por lo tanto, es importante considerar estos factores al utilizar la regla de la suma para calcular probabilidades condicionales. La regla de la suma de probabilidades es un concepto fundamental en la teoría de la probabilidad que se utiliza para determinar la probabilidad de que ocurra un evento u otro.

La regla establece que la probabilidad de que ocurra cualquiera de dos eventos mutuamente excluyentes es la suma de sus probabilidades individuales. Si bien esta regla es muy útil para resolver muchos problemas de probabilidad, también tiene sus limitaciones y desafíos.

En esta sección, discutiremos algunas de las limitaciones y desafíos de la Regla de la Suma. Eventos no mutuamente excluyentes: La regla de la suma solo se aplica a eventos mutuamente excluyentes, lo que significa que la ocurrencia de un evento excluye la ocurrencia del otro.

Sin embargo, en muchas situaciones de la vida real, los eventos no son mutuamente excluyentes y la ocurrencia de un evento no impide que ocurra el otro. En tales casos, no se puede utilizar la regla de la suma y se deben emplear conceptos de probabilidad más avanzados, como la probabilidad condicional o la regla de la multiplicación.

Por ejemplo, considere la probabilidad de sacar una carta roja o una figura de una baraja de cartas estándar. Estos eventos no son mutuamente excluyentes ya que hay 6 cartas con figuras que también son rojas, y la probabilidad de sacar una carta con figuras rojas no es simplemente la suma de la probabilidad de sacar una carta roja y la probabilidad de sacar una carta con figuras.

Eventos superpuestos: a veces, los eventos pueden superponerse y la regla de suma no se puede utilizar directamente. En tales casos, la fórmula de la Regla de Adición debe modificarse para tener en cuenta la superposición. Por ejemplo, considere la probabilidad de sacar una pica o una figura de una baraja de cartas estándar.

Estos eventos se superponen ya que hay 3 figuras que también son espadas. Para calcular la probabilidad correctamente, debemos restar la probabilidad de sacar una figura que también sea una pica.

Eventos dependientes: La regla de la suma supone que los eventos son independientes, lo que significa que la ocurrencia de un evento no afecta la probabilidad del otro. Sin embargo, en muchas situaciones, los eventos son dependientes y la probabilidad de un evento afecta la probabilidad del otro.

En tales casos, no se puede utilizar la regla de la suma y se deben emplear conceptos de probabilidad más avanzados, como la probabilidad condicional o el teorema de Bayes.

Por ejemplo, considere la probabilidad de sacar dos cartas de una baraja de cartas estándar sin reemplazo, donde la primera carta extraída es un corazón. Información limitada: La regla de la suma supone que tenemos información completa sobre los eventos en cuestión, incluidas sus probabilidades.

Sin embargo, en muchas situaciones, es posible que no tengamos información completa y las probabilidades de los eventos pueden ser desconocidas o difíciles de estimar. En tales casos, no se puede utilizar la regla de la suma y se deben emplear conceptos de probabilidad más avanzados, como la estimación de máxima verosimilitud o la simulación de Monte Carlo.

La regla de la suma es una herramienta poderosa para analizar distribuciones de probabilidad, pero tiene sus limitaciones y desafíos. Para utilizar la regla de la suma de forma eficaz, debemos ser conscientes de estas limitaciones y desafíos y estar preparados para utilizar conceptos de probabilidad más avanzados cuando sea necesario.

Limitaciones y desafíos de la regla de la suma - La regla de la suma para probabilidades analisis de distribuciones de probabilidad. Al analizar distribuciones de probabilidad, la regla de la suma de probabilidades es un concepto fundamental que ayuda a determinar la probabilidad de que ocurra un evento.

La regla de la suma establece que la probabilidad de que ocurra cualquiera de dos eventos mutuamente excluyentes es igual a la suma de sus probabilidades individuales. En este blog, exploramos esta regla en detalle y discutimos sus aplicaciones en diferentes escenarios.

En esta sección, resumiremos las conclusiones clave de nuestra discusión y brindaremos algunas ideas. La regla de la suma de probabilidades es un concepto fundamental que ayuda a determinar la probabilidad de que ocurra un evento.

Se basa en el supuesto de que los eventos son mutuamente excluyentes, es decir, no pueden ocurrir simultáneamente. La regla de la suma se puede utilizar para determinar la probabilidad de que ocurra cualquiera de dos eventos.

Si los eventos no son mutuamente excluyentes, debemos utilizar la fórmula de probabilidad condicional para calcular la probabilidad. En este caso, necesitamos sumar las probabilidades de todos los eventos que son mutuamente excluyentes. La regla de la suma se puede aplicar a distribuciones de probabilidad tanto discretas como continuas.

En el caso de una distribución continua, necesitamos utilizar la integración para calcular la probabilidad. La regla de la suma está estrechamente relacionada con el concepto de función de densidad de probabilidad PDF.

La PDF es una función que describe la distribución de probabilidad de una variable aleatoria continua. La regla de la suma se puede utilizar para calcular la probabilidad de una unión de eventos. La unión de dos eventos es el evento en que ocurre cualquiera de los dos eventos.

La probabilidad de la unión de dos eventos es igual a la suma de sus probabilidades individuales menos la probabilidad de su intersección. La regla de la suma también se puede utilizar para calcular la probabilidad de un complemento de un evento.

El complemento de un evento es el evento que no ocurre. La probabilidad del complemento de un evento es igual a uno menos la probabilidad del evento. La regla de la suma para probabilidades es una herramienta poderosa para analizar distribuciones de probabilidad. Ayuda a determinar la probabilidad de que ocurra un evento y se basa en el supuesto de que los eventos son mutuamente excluyentes.

La regla se puede extender a más de dos eventos y se puede aplicar a distribuciones de probabilidad tanto discretas como continuas. Está estrechamente relacionado con el concepto de PDF y puede usarse para calcular la probabilidad de una unión o complemento de eventos.

Comprender la regla de la suma es esencial para cualquiera que trabaje con distribuciones de probabilidad y puede ayudar a tomar decisiones más informadas. Algunas personas disfrutan ensuciándose las manos. Estas son las personas que hacen que las nuevas empresas crezcan tanto. Los Rockies también tienden a ser más ágiles: son el agua que rodea la roca.

Estas son las personas que quieres cuando todo sale mal. También son las personas que quieres a tu lado cuando todo va bien. El espíritu empresarial es el proceso de creación, lanzamiento y gestión de una nueva empresa Al explorar la intersección entre Ayurveda y la tecnología, nos adentramos en el fascinante En el panorama dinámico de la publicidad digital, el arte de la precisión se ha vuelto Si eres como la mayoría de las personas, cuando piensas en la recaudación de fondos, probablemente Siguiente paso:.

Practica las habilidades básicas de la probabilidad en Khan Academy. O mira un video en donde explicamos los fundamentos de la probabilidad. Intro to theoretical probability. O revisa el ejemplo: seleccionar canicas de una bolsa.

Simple probability: yellow marble. Ve todas las lecciones de Khan Academy y haz ejercicios de práctica sobre probabilidad y estadística aquí.

Preguntas Sugerencias y agradecimientos. Inicia sesión. Ordenar por: Más votados. Bañez Salvador. Publicado hace hace 7 años. Voto si quieres que sigan aprendiendo en forma detallada.

Dar voto negativo Botón que navega a la página de registro. Marca Botón que navega a la página de registro. Mostrar vista previa Mostrar opciones de formato Publicar respuesta. Luciano Davila Publicado hace hace 8 meses. pueden votar por mi necesito el logro pls. FERNANDO QUIROZ. Publicado hace hace un año.

Galvez Pongo johana. por que a veces hay ejercicio y otras veces solo lees deberia siempre haber ejercicio en todo.

Joaquin Laos. Publicado hace hace 5 años. La verdad es que se comprende que alla algun error. Comentar Botón que navega a la página de registro. César False. bueno creo que esto no sirvio de algo ¿no? gracias pero no era lo que buscaba :v. Publicado hace hace 6 meses.

Video